Preparing spatial analyses
The most common spatial analyse in forest management planning concern the aggregation of final felled areas. An aggregation could be positive (e.g. when aggregated stands share the fixed costs involved in harvesting) but usually regarded as a problem - large open areas are negative in nature preservation perspectives, in biological diversity matters, etc. "Opening size constrains" are hence often used in a optimization model. Prerequisites for such analyses can be calculated in PlanStart.
NB: "Harvest" is here corresponding to final felling, sometimes also called clearcut. Harvesting is done in thinning but a stand will, after such treatment, not show an open area. A problem occur when seed trees are retained in final fellings. However, the stem density is usually quite low (less than 150 stems per hectare), where quite a few usually will be windthrown in the first couple of years, and hence regarded as an opening.
- Adjacencies
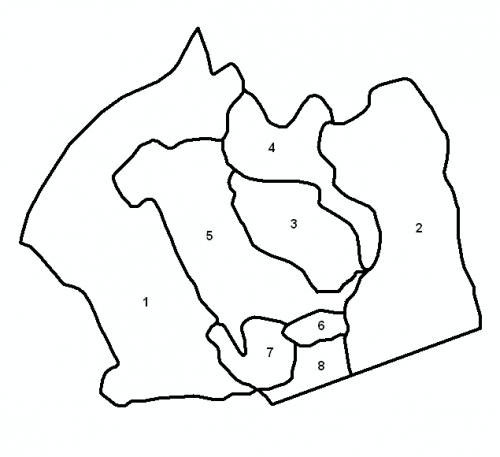
In "Tools" > "Adjacencies..." the analysis area of interest is first selected. By doing this, a problem concering edges occur, and the extent of this problem depends on the selected area. In the figure above, it can be seen that "Landscape8" will suffer from quite extensive edge effects, especially stand number one and two. Any opening sizes including these stands will depend on areas outside the analysis area and any treatments herein.
To each stand, i.e. treatment unit (TU), adjacent stands, called "Neighbours", are derived and the length of the common borders are calculated (in meters). An example of a permutation in this case is CommonBorderLength_TU1_TU2 = CommonBorderLength_TU2_TU1. Another example, stressing the difference between "null" and the value 0 (zero), can be seen in the figure above; stand number eight share common borders with stand two, six, and seven where the length is > 0 meters. But with stand number one this common border length is = 0 meters - the two stands are adjacent in a point only. In later parts of the analyses the user will have to decide if these two areas (of stand number one and eight) should be added or not, if harvested in the same period, to form an opening size. What do you think? How important are, e.g., forested corridors or are your only concern the scenic values?
Adjacencies are a prerequisite in deriving cliques and clusters but can also be used separately in analyzing forest management schemes.
- Cliques and Clusters
In "Tools" > "Compute Cliques and Harvest Clusters" the analysis area is first selected. Adjacencies needs to be calculated prior to this computation. These two parameters might be somewhat tricky to comprehend but necessary in optimizations with opening size constrains. Both cliques and clusters are sets of neighbouring stands, where the sets are defined by the user.
Starting with the harvest clusters (that, by the way, always starts with defining a cluster of each single stand or, more correctly, of each single polygon):
- "Min Border Length" defines the minimum length of a common border (in meters) if the both of two adjacent stands can be included in the same cluster.
- "Max Nb Polygons" defines the maximum number of stands (if the stand correspond to one polygon, else substands = polygons) in a cluster.
- "Max Cluster Area" defines the maximum size (in hectares) of a cluster.
Settings are done partly to limit the amount of data and computational time. By defining a certain "Max Cluster Area", the user can not in later parts restrict any opening sizes above this maximum value. However, it is possible to include restrictions upon opening sizes of lesser size. From this follows that a certain cluster can include two or more other clusters, e.g. the set {TU6, TU7, TU8} at the same time defines the sets {TU6, TU7}, {TU6, TU8}, and {TU7, TU8}, in addition to the clusters of the single stands. A consequence in an optimization model with a certain opening size constrain is that if a cluster can be harvested in a certain period, so can all including clusters be.
Then to the cliques. As said, these consist of sets of stands (or polygons), describing the connection between clusters. The user here defines:
- "Common Border Length > 0 m Required" implies that a point-connection is not enough to include two stands in the same clique.
If the prerequisite above is valid, an example can be seen in the figure: the clique at the border intersection of stand two, three, four, and five equal the sets {TU2, TU4, TU5} and {TU3, TU4, TU5}, else (if a point-connection is enough) the set {TU2, TU3, TU4, TU5}.